Introduction

Risk management in a company is multifaceted. For example, managing "liquidity" risk consists of anticipating and controlling cash flow variations that would result from changes in activity. Managing stocks of materials also involves the same concern. Similarly, an individual seeking to invest his or her money faces investment opportunities that involve risk. Thus, the attitude to risk is one of the fundamental determinants of the demand for financial assets. A european exporter, for example, who sells a dollar-denominated product that will not be paid for until one month from now is exposed to currency risk. If the dollar falls, he loses; if the dollar rises, he gains. In a way, this exporter faces a risk. He can accept it if he is a gambler or if he speculates on the rise, he can on the contrary "hedge", i.e. to ensure himself a given income even if he has to pay for this insurance service. In a way, the exporter above is confronted with a lottery. A simple question that arises is to model how a decision-maker compares two lotteries. A lottery by definition is "risky" income. How does the decision-maker assess this risk? How does he compare two risky situations? This course is intended to model the decision under uncertainty. We will highlight a set of simple instruments widely used to model individual behaviour and decision in front of risk.
Examples
Risk aversion...
To understand investors' attitudes to risk, it is useful to consider an extremely simple textbook case. We consider two lotteries called lottery \(a\) and lottery \(b\). In the first lottery, \(a\), you win 2 euros with a 1 in 2 chance, and you win 0 euros with 1/2. In the second lottery, \(b\), you win for sure \(\beta\) euros.
| probabilities | \(\frac{1}{2}\) | \(\frac{1}{2}\) |
| payoff of lottery \(a\) | 2 | 0 |
| payoff of lottery \(b\) | \(\beta\) | \(\beta\) |
If an individual is asked to choose which lottery he prefers to play, his answer will obviously depend on both his "attitude" to risk and the value of \(\beta\). Certainly, however, some of the values of \(\beta\) do not pose a problem. For example, clearly, if \(\beta = 0\), everyone will prefer to play the lottery \(a\)! Similarly, if \(\beta = 2\), everyone will choose the lottery \(b\)! We can thus affirm, by a continuity reasoning, that there is a threshold level \(\widehat{\beta}\), which is a priori different depending on the individual, such as: \(\beta <\widehat{\beta} \) then the individual chooses \(a\), when \(\beta >\widehat{\beta} \) the individual chooses \(b\) and when \(\beta=\widehat{\beta} \) the individual is indifferent. In a way, the threshold value gives an indication of the degree of risk aversion of our individual. If \(\widehat{\beta} \) is very small, our man prefers safe things! If \(widehat{\beta} \) is very big, it takes a lot of money to dissuade him from gambling! The position of \(\widehat{\beta} \) in relation to the lottery \(a\) expected value , equal to \(\mathbb{E}(a) = \frac{1}{2} \times 2 + \frac{1}{2}\times 0 = 1\), gives an information:
- - We'll say the individual is risk-averse if \(\widehat{\beta} < 1\),
- risk-lover if \(\widehat{\beta} > 1\),
- and risk-neutral if \(\widehat{\beta} = 1\).
In the next chapter we will study two (dual) ways to modelize risk aversion. In some sense, an individual will be highly risk-averse if he is ready to pay a large amount of money to reduce risk, that is to replace a random income by a sure one equal to the mean.
... Diversification
One very usual way to reduce risk is diversification : Don't put one's eggs in the same basket.
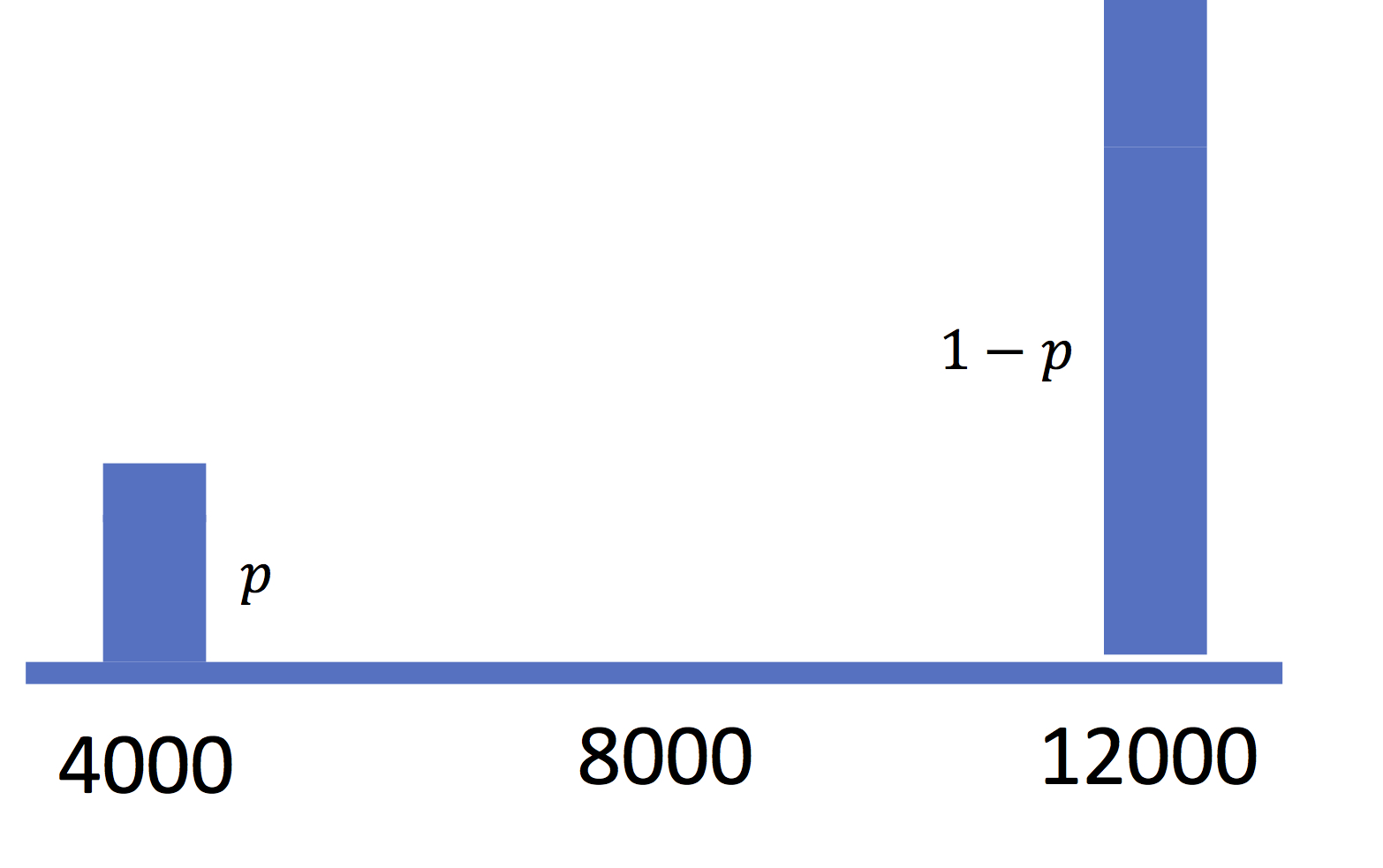
Bernoulli (Daniel), a famous Swiss mathematician, wrote in 1738 an article (in Latin!) "on a new theory of risk measurement" (specimen theoriae novae de mensura sortis) in which he tells the story of a certain Sempronius, a sort of international trader. Here is what Bernoulli writes (translated): "Sempronius holds 4,000 ducats at home and, in addition, possesses 8,000 ducats of goods abroad that can only be repatriated by ship. It so happens, however, that a ship has a one in ten chance of sinking during the voyage". In today's language, it seems that Sempronius is exposed to a risk to his wealth. The lottery to which he is exposed can be represented by the vector (\((4000,p = 0.1), (12000, 1 - p = 0.9)\)) and graphically represented by the distribution. In expectation, its richness is equal to \(4000 + 0.9 × 8000 + 0.1 × 0 = 11200\) ducats.
Sempronius then has a brilliant idea: instead of taking only one boat he distributes his wealth over two. Assuming that the ships followed equally dangerous but independent routes, he will loose the 8000 ducats if both ships sink, 4000 if only one of them sinks, 0 if both arrive safely. The lottery (its final wealth) then becomes (\((4000,0,01 = p^{2}),(8000,0,18 = 2p(1 - p)), (12000,0,81 = (1 - p)^{2})\)) represented by the green distribution. In expectation Sempronius neither wins nor loses, but one has the intuition that the risk to which his fortune is exposed has decreased: the probability of extreme events has decreased in favour of the increase of an intermediate event. This type of phenomenon is central in an economy of uncertainty and we will see how to generalize it.
Diversification : mass transportation
In the first panel is represented the distribution of
probablity of Sempronius wealth if he loads only one boat
:
\((4000,p = 0.1), (12000, 1 - p = 0.9)\)
.
With probability \(p\) he looses 8000 ducats, so that he
get 12000-8000=4000.
In the second panel is represented the distribution of
probability of his wealth if he charges two (independent)
boats. He looses the 8000 ducats if both ships sink, 4000
if only one of them sinks, 0 if both arrive safely. So
that the distribution is :
\((4000,0,01 = p^{2}),\)
\((8000,0,18 = 2p(1 - p)), (12000,0,81 = (1 - p)^{2})\).
The mean remains the same but the distribution is more
concentrated.
This diversification amounts to mass transportation from
extreme to the center (third panel).
... Mutualization
On an exotic island, which we will call Febooupa the weather
regime is such that when the weather is good on the East coast (E)
it is bad on the West coast (W) and vice versa. Obviously the
weather is random. At each tourist season, either the weather is
good in the West (and bad in the East) and tourist activities in
the West are flourishing (in the East, on the contrary, business
is bad), or it's the opposite.
We are here in the presence of a "pure randomness": the resources
on each side of the island are random. Here, two points of view
are possible: from the point of view of individuals on each side,
his or her resource is random and "there is nothing to be done".
From the global point of view things are less risky: when one has
resources the other does not and vice versa.
We can then see that we can "mitigate" the risk for each side: the total resource (the sum of the resources of the East and the West) is not random! The introduction of financial assets helps to improve the situation. For example, an insurance company can offer an insurance contract that compensates in case of bad weather. Another way of doing this is to list each of the two companies on the stock exchange: the West side then takes stakes in the East side and vice versa (cross shareholdings). It is clear that a financial contract between the two sides of the island can reduce and even completely eliminate the risk! There are even several types of contracts that make it possible to do this: an insurance contract or an exchange of shares.
Obviously this is an extreme case where risks are perfectly
anticorrelated so that the total wealth is sure. But in general,
mutualization allows to reduce individual risks. For example, for
idendically distributed and independent variables with finite
means \(\widetilde{w}_{i}\) one can show that
\(\frac{\sum_{j=1}^{n}\widetilde{w}_{i}}{n}\) is "less
risky" (the distribution is more concentrated as in the Sempronius
storie's case) than each \(\widetilde{w}_{i}\). For
instance if \(\widetilde{w}_{i}\) are gaussian with mean
\(m\) and standard error \(\sigma\), \(\frac{\sum_{j=1}^{n}\widetilde{w}_{i}}{n}\)
is also gaussian with the same mean and with standard error
\(\frac{\sigma}{\sqrt{n}}\).
Exchange of risk:the price of risk
Obviously, the case where the exposition to risk is identical among individuals is a particular case.
Instead, consider the following story.
Alice is an entrepreneur. Her activity provides her a random net income (profit). There are two ``states of nature'' (events) : the good state where the income is large, business is flourishing, \(w_{h}\) and the bad state where it is low \(w_{\ell} < w_{h}\).
Bob is a salaried man who has a constant income \(w_{0}\).
| probability | \(\pi_{\ell}\) | \(\pi_{h}=1-\pi_{\ell}\) |
| Alice's income | \(w_{\ell}\) | \(w_{h}\) |
| Bob's income | \(w_{0}\) | \(w_{0}\) |
In this economy the total income is hence \(w_{h}+w_{0}\) or \(w_{\ell}+w_{0}\). Alice has a real initial "position" : she is exposed to a risk and, that will be a permanent assumption, would like to mitigate it, that is to reduce its variability. That means that she would like to have a final income \(x\) such that \(x_{h}\) (final income when the statee is \(h\) is not very different than \(x_{\ell}\) (final income when the state is \(\ell\).
Alice can try to trade with Bob by selling him some share of her firm.
The proposed deal is that she sells a share \(\alpha\) at a unit price \(p\). If so the final situation will be :
- Alice will have \(x_{\ell}=\alpha p+(1-\alpha)w_{\ell}=w_{\ell}+\alpha\left(p-w_{\ell}\right)\) and \(x_{h}=\alpha p+(1-\alpha)w_{h}=w_{h}+\alpha\left(p-w_{h}\right)\)
- And Bob :\(y_{\ell}=w_{0}-\alpha\left(p-w_{\ell}\right)\) and \(y_{h}=w_{0}-\alpha\left(p-w_{h}\right)\)
| After deal \(\alpha,p)\) | state : \(\ell\) | state \(h\) |
| Alice's income | \(x_{\ell}=w_{\ell}+\alpha\left(p-w_{\ell}\right)\) | \(x_{h}=w_{h}+\alpha\left(p-w_{h}\right)\) |
| Bob's income | \(y_{\ell}=w_{0}-\alpha\left(p-w_{\ell}\right)\) | \(y_{h}=w_{0}-\alpha\left(p-w_{h}\right)\) |
But to Bob has to accept the deal. For him buying \(\alpha\) shares increases the risk. If he has risk aversion, which is a permanent assumption, he will accept to increase his risk to the condition that his average (expected) income increases. For a deal \(\alpha\) at price \(p\)
the expected value of Bob's income is :
\(\pi_{\ell}y_{\ell}+\pi_{h}y_{h}=w_{0}+\alpha\left[\pi_{\ell}w_{\ell}+\pi_{h}w_{h}-p\right]\)
It follows that the price must be lower than the expected value of Alice's initial income!
Bevause of risk aversion, Alice, too, will be ready to sell her firm at a price lower than the expected value of income.
So that we conclude that risk exchange is possible even between risk averse agents.
For a given price, \(p\), we define the supply \(\alpha^{s}\left(p\right)\) being the share that Alice is ready to offer at that price, and the demand \(\alpha^{d}\left(p\right)\), as the share, Bob is ready to buy at this price.
The equilibrium value \(p^{*}\) is the level of price \(p\) such that the demand is equal to the supply. This price will be lower than \(\pi_{\ell}w_{\ell}+\pi_{h}w_{h}\).
We will see in the sequel how to generalize that kind od result.
e-book content
The first chapter is devoted to risk measurement. We define risk measures based on quantile function. Then we define utility indexes and relate them to stochastic dominance
The second chapter is devoted to risk aversion in the expected utility approach.
The third chapter is devoted to portfolio choice and insuranse demand in the expected utility approach.
The fourth chapter is devoted to information and risk.