T1
Chapitre
1 Introduction à la théorie des jeux
1. Introduction
Il existe de multiples exemples, dans le domaine de l’économie, mais aussi plus largement, dans un grand nombre d’activités humaines, de situations dans lesquelles il existe une interaction entre différents acteurs, c’est à dire lorsque le résultat d’un processus dépend le l’ensemble des actions prises par différents agents. L’objet de la théorie des jeux est la formalisation de ces interactions pour tenter (approche positive) d’en prédire l’évolution, ou (approche normative) de conseiller le ou les joueurs sur le meilleur coup à jouer. L’exemple emblématique de jeu est le « jeu de société » : la règle du jeu spécifie les actions possibles et leur résultats. Aux échecs par exemple le résultat dépend de ce que jouent les blanc et les noirs en respectant les modes de déplacement des pièces.
Un jeu peut comporter un conflit d’intérêt, c’est-à-dire une situation dans laquelle il y a antagonisme dans les issues. Mais il peut aussi comporter de la convergence d’intérêts, et le problème qui se pose est alors celui de la coordination des actions.
Nous raisonnons ici dans un cadre dit « non coopératif ». Autrement dit les acteurs sont supposés prendre leurs décisions librement sans possibilité de concertation et d’engagement a priori.
2. Jeux (sous forme extensive)
Représentation
Définition
1 : arbre du jeu
•
arbre (graphe connexe sans cycle) représentant les déroulements possibles du
jeu.
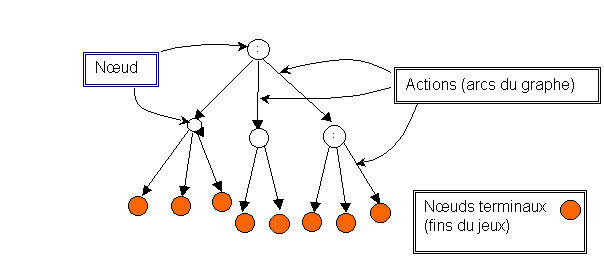

•
à chaque noeud non
terminal est associé un joueur : arrivé à ce point du jeu c'est à son
tour de jouer.
•
Chaque arc représente
chacune des actions (coups autorisés par la règle) que ce joueur peut prendre
à ce point du jeu.
•
à chaque noeud
terminal correspond un résultat du jeu donné de manière générale par un
vecteur dit vecteur des paiements (liste des gains attribués à chaque joueur).
Définition
2 : jeu fini en information parfaite
un jeu sous forme
extensive, en information parfaite, est défini par:
–
l'ensemble des joueurs
![]()
–
l'arbre du jeu
: constitué d'un ensemble fini de noeuds ![]() muni d'une relation
de "succession".
muni d'une relation
de "succession".
•
le noeud initial (début
du jeu) n'est le successeur d’aucun autre nœud.
•
chaque noeud (non
initial) est le successeur d’un seul nœud.
•
Les noeuds terminaux
n'ont pas de successeurs
(on note s(t),
l'ensemble des successeurs d'un noeud t)
–
à chaque noeud t (non terminal) est associé un joueur
i(t). A ce point du jeu
c'est à i(t) de jouer.
–
A chaque noeud t
est associé un ensemble d'actions A(t) ,
à chaque action correspond un noeud successeur unique dans s(t).
– A chaque noeud terminal z est associé un vecteur des paiements. u(i,z) est le gain du joueur i si le jeu se termine au noeud z.
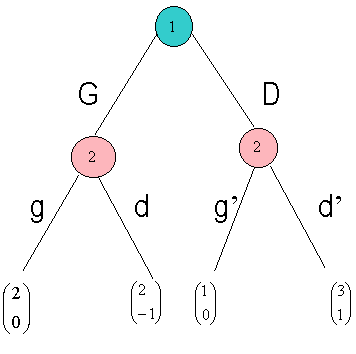
Exemple 1
Dans le jeu
ci-contre : -
lorsque 1 joue G
et 2 joue g, les gains sont 2 pour le joueur 1 et 0 pour le joueur 2. -
lorsque 1 joue G et
2 joue d, les gains sont 2 pour le joueur 1 et -1 pour le joueur 2. -
lorsque 1 joue D
et 2 joue g’, les gains sont 1 pour le joueur 1 et 0 pour le joueur 2. -
lorsque 1 joue D
et 2 joue d’, les gains sont 3 pour le joueur 1 et 1 pour le joueur 2.
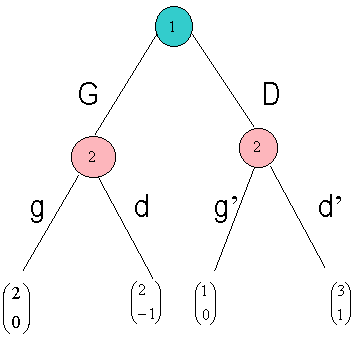

Remarque : le
joueur 2 observe ce qu’a joué le joueur 1 !
De
nombreux jeux entrent dans cette catégorie, évidemment les graphes associés
peuvent être plus ou moins compliqués !
(un site de
jeux… : cliquer
ici)
Information
imparfaite
Pour prendre en
compte les situations dans lesquelles un joueur n’a pas les moyens d’observer
certaines des actions d’un autre joueur, on introduit la notion d’ensemble
d’information :
Définition :
Un ensemble d’information est un ensemble de nœuds indiscernables pour le
joueur à qui c’est le tour de jouer. Evidemment, en deux nœuds appartenant à un
même ensemble d’information, les actions possibles doivent être strictement les
mêmes (sinon les nœuds ne seraient pas indiscernables).
Exemple 2
Le joueur 2 ne
sait pas ce qu’a joué 1. Tout se passe comme si 1 et 2 jouaient
simultanément
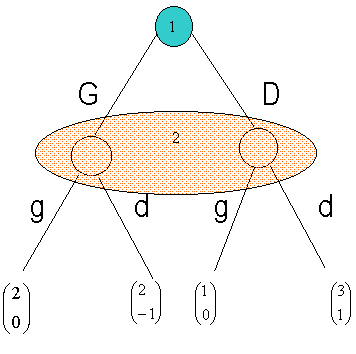

3. Forme normale d’un jeu
Stratégies et forme normale
Définition 3 :
stratégies et forme normale
- une stratégie
(ex ante) est la donnée d’une liste des actions qu’un joueur projette de jouer
à chacun des nœuds (ou ensembles d’information) où il aura potentiellement la
main. On note ![]() l’ensemble des
stratégies du joueur i
pour le jeu donné.
l’ensemble des
stratégies du joueur i
pour le jeu donné.
- Un jeu sous forme
normale est défini par
-
N, ensemble des joueurs
-
![]() , l’ensemble des stratégies
, l’ensemble des stratégies
-
Les fonctions de paiement qui spécifient le gain de chaque joueur en
fonction des stratégies jouées par l’ensemble des joueurs :
![]()
Un jeu sous
forme normale sera ainsi noté G(N,X,![]() )
)
Il est important de
noter qu’une stratégie est un objet « compliqué » au sens où le
joueur définit l’ensemble des actions qu’il prendra en tout point où il aura la
main !
Tout se passe comme
si le joueur devait programmer une machine pour jouer à sa place : il ne
doit pas laisser de situations imprévues (y compris celles qui pourraient
apparaître absurdes !)!
Il est usuel de
représenter un jeu fini à deux joueurs
sous forme normale par le tableau des gains. Pour le jeu de l’exemple 1 la
forme normale s’écrit :
Exemple 1
|
|
||||
|
G |
2 0 |
2 0 |
2 -1 |
2 -1 |
|
D |
1 0 |
3 1 |
1 0 |
3 1 |
Pour celui de
l’exemple 2 :
Exemple 2
|
|
g |
d |
|
G |
2 0 |
2 -1 |
|
D |
1 0 |
3 1 |
Exercice 1: cliquer ici
Jeux à deux joueurs à somme nulle
Définition :
On dit qu’un jeu
à 2 joueurs est à somme nulle si :
![]()
Ainsi, ce que gagne l’un est perdu par l’autre.
Lorsque le
résultat du jeu pour un joueur est le gain la perte ou la partie nulle (sans
spécification du montant en jeu), on
écrit ![]() ou 0.
ou 0.
4. Le problème stratégique
Ayant ainsi défini
un jeu sous forme extensive puis sous
forme normale, la première question qui se pose est simple : peut-on
raisonnablement prédire les comportements qui vont être adoptés par les
joueurs ? Le caractère « interactif » d’un jeu implique que la
réponse à cette question n’est pas immédiate. Dans un jeu à deux joueurs par exemple,
chaque joueur se pose la question de savoir quelle stratégie sera adoptée par
l’autre pour réagir en conséquence. Mais il sait que l’autre est dans la même
situation.
Comportement prudent
L’analyse d’un jeu
à somme nulle permet de mettre en évidence le type de problème rencontré.
Imaginons le
raisonnement suivant du joueur 1. Si je joue la stratégie ![]() et que l’autre le
sache, il jouera en conséquence, c'est-à-dire qu’il adoptera une stratégie qui
maximise son gain pour
et que l’autre le
sache, il jouera en conséquence, c'est-à-dire qu’il adoptera une stratégie qui
maximise son gain pour ![]() . Comme le jeu est à somme nulle, il choisira une stratégie
qui minimise en y
. Comme le jeu est à somme nulle, il choisira une stratégie
qui minimise en y ![]() (en supposant qu’une telle stratégie
existe). J’obtiendrai ainsi
(en supposant qu’une telle stratégie
existe). J’obtiendrai ainsi ![]() . Mon choix
est alors très simple : j’adopterai une stratégie qui maximise
. Mon choix
est alors très simple : j’adopterai une stratégie qui maximise ![]() , et j’obtiendrai ainsi
, et j’obtiendrai ainsi ![]() . Remarquons ici, que tout se passe comme si 1 jouait
« en premier » et adopte la meilleure stratégie qui tienne compte de
la réponse optimale de 2.
. Remarquons ici, que tout se passe comme si 1 jouait
« en premier » et adopte la meilleure stratégie qui tienne compte de
la réponse optimale de 2.
Définition 4: stratégies
prudentes
Dans un jeu à
somme nulle, on appelle « paiement minimum garanti du joueur 1» la
valeur de ![]() . C’est effectivement le paiement minimum garanti dans le sens
ou il existe une stratégie qui assure ce paiement au joueur, cette stratégie
. C’est effectivement le paiement minimum garanti dans le sens
ou il existe une stratégie qui assure ce paiement au joueur, cette stratégie ![]() , est appelée stratégie prudente.
, est appelée stratégie prudente.
Un autre
raisonnement est cependant possible. Le joueur 1 peut parfaitement se dire que
2 tiendra exactement le raisonnement précédent! Tout se passe alors comme si 1 jouait en second. Si 2 joue y j’ai intérêt à répondre une stratégie qui
maximise en x ![]() . J’obtiendrai alors
. J’obtiendrai alors ![]() , alors que 2 obtiendra
, alors que 2 obtiendra![]() . Je peux en déduire que 2 aura intérêt à jouer une stratégie
qui maximise
. Je peux en déduire que 2 aura intérêt à jouer une stratégie
qui maximise ![]() . 2 obtiendra alors
. 2 obtiendra alors ![]() , et j’obtiendrai donc
, et j’obtiendrai donc ![]() .
.
Remarque : il
est facile de voir que l’on a ![]()
Deux cas de figure
peuvent alors se présenter. Si ![]() , c'est-à-dire si
, c'est-à-dire si ![]() , les deux raisonnements sont « compatibles » et on peut imaginer que chacun des deux joueurs
vont adopter une stratégie « prudente ». Sinon,
, les deux raisonnements sont « compatibles » et on peut imaginer que chacun des deux joueurs
vont adopter une stratégie « prudente ». Sinon, ![]() , il y a conflit entre les deux raisonnements, chacun
aimerait pouvoir jouer en second !
, il y a conflit entre les deux raisonnements, chacun
aimerait pouvoir jouer en second !
5. Elimination des stratégies dominées
Stratégies dominées
Prédire le comportement est ainsi chose difficile. On peut cependant sérier les problèmes et tenter de proposer certains principes de comportement raisonnables.
D’une manière
générale, on peut se poser une première question : existe-t-il des
stratégies qui n’ont aucune chance d’être jouées rationnellement par les
joueurs.
Définition 5 : Dominance
Etant donné un
jeu sous forme normale G(N,X,![]() ),
),
On dit que la
stratégie ![]() est strictement
dominée par la stratégie
est strictement
dominée par la stratégie ![]() pour le joueur
i si et seulement si :
pour le joueur
i si et seulement si :
![]() que l’on peut réécrire sous une forme plus
lisible :
que l’on peut réécrire sous une forme plus
lisible :![]()
Contre toute
« défense », jouer la stratégie ![]() donne toujours strictement
plus au joueur i que jouer
donne toujours strictement
plus au joueur i que jouer ![]() .
.
On dit que la
stratégie ![]() est faiblement
dominée par la stratégie
est faiblement
dominée par la stratégie ![]() pour le joueur
i si et seulement si :
pour le joueur
i si et seulement si :
![]() que l’on peut réécrire sous une forme plus
lisible :
que l’on peut réécrire sous une forme plus
lisible :![]()
Contre toute
« défense », jouer la stratégie ![]() donne toujours au
moins autant au joueur i que jouer
donne toujours au
moins autant au joueur i que jouer ![]() .
.
On dit que la
stratégie ![]() est dominée
par la stratégie
est dominée
par la stratégie ![]() pour le joueur
i si et seulement si :
pour le joueur
i si et seulement si :
![]() que l’on peut réécrire sous une forme plus
lisible :
que l’on peut réécrire sous une forme plus
lisible :![]()
avec une
inégalité stricte au moins.
Contre toute « défense », jouer la stratégie ![]() donne toujours autant
et au moins une fois plus au joueur i que jouer
donne toujours autant
et au moins une fois plus au joueur i que jouer ![]() .
.
On dit qu’une
stratégie est dominante si elle domine toutes les autres. Si une stratégie
dominante existe elle est évidemment unique, en effet si deux stratégies
étaient simultanément dominantes elles donneraient les mêmes paiements au
joueur, ce qui contredit l’existence d’une inégalité stricte au moins. En
revanche, il peut parfaitement exister plusieurs stratégies (faiblement
dominantes).
Il est clair que si
un joueur possède une stratégie dominante il la jouera et le jeu sera résolu.
En revanche la faible dominance peut ne pas déboucher….
Le jeu
emblématique : dilemme du prisonnier (A est une stratégie dominante pour
chacun)
|
|
A |
P |
|
A |
0 0 |
2 -1 |
|
P |
-1 2 |
1 1 |
Le renvoi
d’ascenseur (toutes les stratégies sont faiblement dominantes, elles ne
sont pourtant pas équivalentes!):
|
|
G |
D |
|
H |
0 0 |
1 0 |
|
B |
0 1 |
1 1 |
Exercice : cliquer ici
Algorithme d’élimination des stratégies dominées
Une idée à première
vue assez simple, consiste à remarquer qu’un joueur ne jouera certainement pas
une stratégie strictement dominée. Cette remarque de bon sens va
pourtant assez loin. Chaque joueur peut faire se raisonnement et ainsi effacer
de la forme normale les lignes et les colonnes qui correspondent à des
stratégies strictement dominées. Mais une fois ce premier nettoyage réalisé, il
est possible que des stratégies (non dominées initialement) le deviennent de
sorte qu’un second nettoyage s’impose. Cet algorithme d’élimination successive
peut être fait par chacun des joueurs. Si cet algorithme converge en un
singleton.
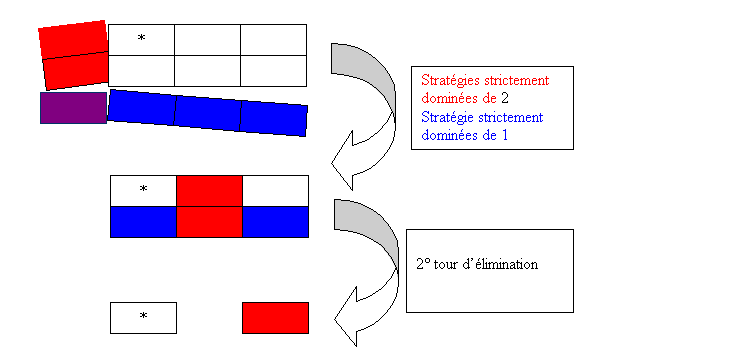

L’élimination
successive des stratégies strictement dominées ne dépend pas de l’ordre
d’élimination, ni du fait que les joueurs éliminent de façon séquentielle ou
simultanée. Elle converge vers un jeu réduit, qui est bien défini. Si c’est un
singleton (une seule stratégie pour chacun) on a un candidat à un équilibre
évident.
On peut concevoir
le même raisonnement en éliminant les stratégies dominées (non strictement).
Dans ce cas l’algorithme peut dépendre de l’ordre et de la manière dont les
joueurs éliminent.
Exemple
Chaque joueur doit
donner un nombre entier entre 0 et 100, on calcule la moyenne, le gagnant est
celui dont le pari est le plus proche de la demi-moyenne.
5. Equilibres de Nash
Evidemment, les
concepts précédents peuvent ne rien donner. Si aucune stratégie n’est dominée,
le problème reste entier. Un concept plus faible permet, dans un grand nombre
de cas une résolution intéressante des
jeux.
Définition 6: meilleure réponse
Correspondance
de meilleure réponse. On
appelle correspondance de meilleure réponse du joueur i la correspondance qui à
chaque vecteur de stratégies des autres joueurs associe les stratégies qui
maximisent le paiement de i :
![]()
Cette
correspondance est bien définie dès lors que, par exemple l’ensemble des
stratégies est fini, ou bien lorsque l’ensemble des stratégies est compact et
la fonction ui
continue. C’est une fonction lorsque le maximum est unique. C’est le cas lorsque
la fonction ui est strictement concave.
Un équilibre de
Nash est un point fixe de la
correspondance de meilleure
réponse :
Définition 7: Equilibre de Nash (John Nash)
![]() est un équilibre de Nash si et seulement
si :
est un équilibre de Nash si et seulement
si :
![]()
c'est-à-dire :
![]()
Il est facile de
voir qu’il existe des jeux pour lesquels il n’existe pas d’équilibre de Nash,
d’autres où il en existe plusieurs.
Exemples :
« Pierre, ciseaux, papier » :
Les ciseaux coupent le papier qui emballe la pierre qui casse les
ciseaux !
Pas d’équilibre de
Nash
|
|
C |
||
|
P |
0 0 |
1 -1 |
-1 1 |
|
C |
-1 1 |
0 0 |
1 -1 |
|
F |
1 -1 |
-1 1 |
0 0 |
Carrefour :
deux voitures arrivent à une intersection, et il n’y a ni feu rouge ni règle de
priorité…. 2 équilibres (Passe, Stop) et (Stop, Passe)
|
|
Passe |
Stoppe |
|
Passe |
-1 -1 |
2 1 |
|
Stoppe |
1 2 |
0 0 |
Bataille des
sexes :
Le mari et la femme
doivent se retrouver au spectacle ce soir, mais ils ne savent pas si c’est au Théâtre
ou à la Boxe, et ils ne peuvent communiquer !
(2
équilibres !)
|
|
T |
B |
|
T |
3 2 |
1 1 |
|
B |
1 1 |
2 3 |
Dans le dilemme du
prisonnier (cf plus haut) il existe un équilibre de Nash unique (c’est évidemment
l’équilibre en stratégies dominantes). Cet équilibre est très peu
efficace : une coordination sur (P,P) donne plus à chacun des joueurs.
Existence d’un équilibre de Nash
L’existence d’un
équilibre de Nash dans un jeu est liée à l’existence d’un point fixe dans la
correspondance de meilleure réponse. Les théorèmes de points fixes permettent
ainsi de caractériser les situations dans lesquelles un équilibre existe. Le
résultat le plus communément utilisé est le suivant :
Théorème
1
- Si les ensemble
de stratégies sont des Convexes, compacts,
- Si les
fonctions de paiement sont quasi-concaves et continues
alors il existe
un équilibre de Nash.
Le théorème
précédent permet d’assurer l’existence d’un équilibre de Nash si l’on autorise
les stratégies « mixtes » dans les jeux finis. On dit qu’un
joueur joue une stratégie mixte lorsqu’il tire au sort, selon une loi donnée,
entre ses différentes stratégies, les paiements associés étant simplement les
espérances de paiement. Si un joueur dispose de p stratégies, l’exemple des
stratégies mixtes est l’ensemble des p-uplets de nombres positifs et inférieurs
à 1 dont la somme est 1. Cet ensemble est un convexe compact. Dans le jeu
Pierre Ciseau Feuille, jouer avec une probabilité 1/3 P, C et F est un équilibre
de Nash.
6. Equilibre Parfait
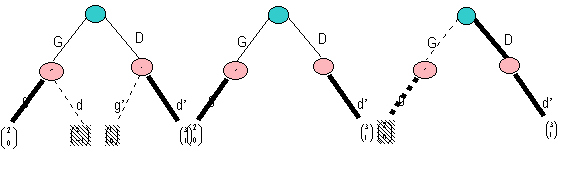
Reprenons l’exemple 1, et cherchons les
équilibres de Nash. Les meilleures réponses sont les suivantes :

gg’![]() G
G![]() {gg’,gd}
{gg’,gd}
dd![]() D
D![]() {dd’,gd’}
{dd’,gd’}
gd’![]() D
D![]() {dd’,gd’}
{dd’,gd’}
dg’![]() G
G![]() {gg’,gd’}
{gg’,gd’}
Il existe 2
équilibres de Nash : (gg’,G) qui
aboutit au paiement (2,0) et (dd’ ou gd’,D) qui aboutit à (3,1).
Le premier équibre
de Nash repose sur un comportement quelque peu surprenant : 2 joue gg’
c'est-à-dire qu’il « annonce » qu’il jouera g’ si 1 joue D. Ce qui
n’est pas très rationnel puisque si 1 joue D, 2 a strictement intérêt à jouer
d’ ! Cet équilibre de Nash repose ainsi sur une menace non crédible.
Comment faire pour éviter ce genre de résultat. L’idée est simple, il faut
demander que la stratégie soit séquentiellement rationnelle : elle
doit prévoir un comportement « optimal » en tout point de l’arbre,
c'est-à-dire même en dehors de la trajectoire qui sera jouée à
l’équilibre : 1 peut raisonnablement anticiper que 2 jouera d’ (et pas g’)
s’il joue D, et anticiper qu’il jouera g s’il joue G. Il en résulte qu’il doit
comparer l’issue Gg’ à Dd’ et donc
choisir de jouer D (ce qui correspond au second équilibre de Nash).
Algorithme de Kuhn dans un jeu à information parfaite
Le raisonnement
précédent peut être généralisé à tout jeu fini en information parfaite.
L’algorithme est le suivant :
Plaçons nous en fin
de jeu, en un nœud prédécesseur d’un nœud terminal. Imaginons que le déroulement
du jeu conduise à ce point. On peut anticiper que le joueur en question, jouera
de manière optimale et choisira l’action (on suppose ici qu’il n’y a pas
d’indifférence pour simplifier) qui
maximise son gain. On peut donc effacer les autres actions issues de ce noeud.
Le comportement devient d’une certaine manière totalement prévisible et on peut
remplacer le noeud en question par le nœud terminal (avec les paiements correspondants) associé à l’action
optimale. On recommence la procédure d’analyse pour les autres nœuds qui
précèdent immédiatement les nœuds terminaux. A chaque étape de
l’algorithme, l’arbre est (strictement)
réduit. Si l’on répète l’opération on débouche nécessairement sur le nœud
initial. Le jeu est réduit à un problème de décision simple du premier
joueur !
Définition 8 : Equilibre parfait
Equilibre parfait
dans un jeu sous forme extensive en information parfaite.
Le résultat de l’algorithme
de Kuhn est appelé équilibre parfait.
Remarquons qu’il
existe toujours au moins un équilibre parfait pour ce type de jeu :
l’algorithme de Kuhn converge toujours.
Remarquons aussi
qu’algorithme de Kuhn et élimination des stratégies dominées sont deux
procédures très similaires. On peut montrer facilement qu’un équilibre par
élimination des stratégies dominées est un équilibre parfait. En revanche la
réciproque n’est pas toujours vraie, il suffit pour s’en convaincre de
remplacer le paiement 3 par le paiement 2 dans le jeu précédent : il
existe alors deux équilibre parfaits (Dd’, mais aussi Gg), alors que l’issue Gg
ne peut être obtenue par élimination des stratégies dominées. En revanche les
deux concepts coïncident dès lors qu’il n’y a pas d’indifférence (et donc
d’ambiguïté dans l’algorithme de Kuhn).
Exercice : cliquer ici
Equilibre parfait en sous jeux
Le concept
précédent peut être généralisé dans le cas de jeux sous forme extensive en
information imparfaite. L’idée est simple : l’algorithme de Kuhn est
fondée sur l’idée de cohérence interne : chaque joueur anticipe pour toute suite possible que les
autres joueraient de manière optimale s’ils étaient conduits à cette séquence
du jeu. Peut-on transposer cette idée à des jeux où il existe des ensembles
d’information non réduits à des singletons ?
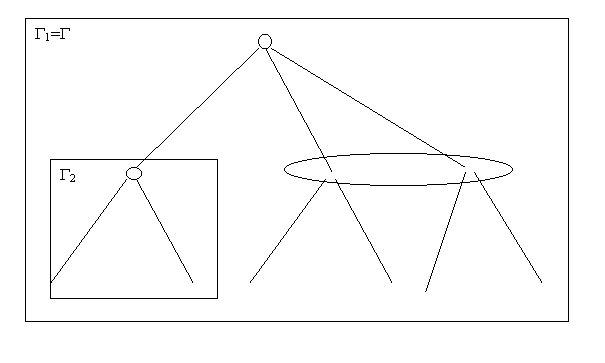
Définition
9 : Sous-jeu
On appelle
sous-jeu d’un jeu donné, le jeu défini par un sous-arbre commençant en un
ensemble d’information réduit à un singleton.
Exemple : deux
sous-jeux.

Définition 10 : Equilibre parfait en
sous-jeux
Un équilibre
parfait en sous-jeux (ou Nash parfait) d’un jeu (sous forme extensive) est constitué
de stratégies qui sont en équilibre de Nash dans tous les sous-jeux.
Remarque : lorsqu’un sous-jeu est réduit à un jeu à 1
joueur, le concept d’équilibre de Nash est dégénéré, la stratégie doit
simplement prévoir un comportement optimal.
Remarque : Le concept d’équilibre parfait en sous-jeux
coïncide avec celui d’équilibre parfait lorsque le jeu est en information
parfaite.
Exemple : jeu en deux étapes
(information presque parfaite)
Un jeu à deux
joueurs, en deux étapes (ou périodes) se déroule de la manière suivante. Dans
une première période chacun des deux joueurs choisit une stratégie Ki. Au début de la seconde étape chacun
observe les choix opérés en première et doit choisir une action de deuxième
étape xi. Les
paiements finaux sont ui(K1,K2,x1,x2).
Pour chaque couple K1,K2, on cherche les équilibres de Nash en x1,x2. Notons un équilibre de Nash de ce sous-jeu
![]() . Un équilibre de Nash parfait doit être tel que les stratégies
de première période constitue un équilibre de Nash du jeu ayant les paiements
. Un équilibre de Nash parfait doit être tel que les stratégies
de première période constitue un équilibre de Nash du jeu ayant les paiements ![]() .
.
7. Equilibre Bayesien Parfait
Dans le concept
précédent, un sous-jeu commence en un ensemble d’information singleton. Dans l’exemple de la définition, par exemple,
il n’y a que deux sous jeux. En un ensemble d’information non réduit à un
singleton, il n’est pas en général possible de mettre en œuvre l’algorithme de
Kuhn (sauf, s’il existe une stratégie dominante…). Prenons l’exemple
suivant (on ne mentionne que les paiements du joueur en question):
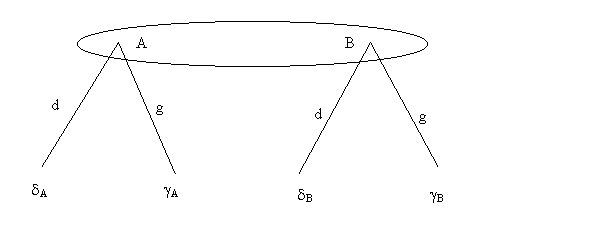

Evidemment, si dA>gA
et dB>gB (ou dA<gAet dA<gA) le problème du joueur est trivial. En
revanche on ne peut rien dire lorsque on a par exemple
dA>gA et dB<gB, sauf si l’on fait une hypothèse sur les
probabilités respectives des nœuds A et B. Si il y a de grandes chances d’être en
A, le joueur jouera d. On voit ainsi que l’on peut « généraliser
l’algorithme de Kuhn » à condition
d’affecter des probabilités aux nœuds des ensembles d’information et de
remplacer les gains par les espérances de gain associées. On appelle
croyances ces probabilités. A croyances
données mA
et mB=1-mA, on peut remplacer le morceau d’arbre
précédent par :
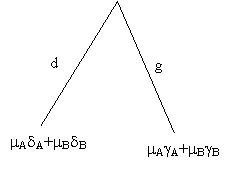
Si l’on opère de la
même façon pour tous les ensembles d’information, on peut mettre en œuvre l’agorithme
de Kuhn et déboucher sur un équilibre !
Evidemment
l’équilibre trouvé dépend des
croyances. A croyance donnée on a un equilibre :
![]()
Cet équilibre donne
les stratégies que doivent suivre les joueurs. Si ces stratégies sont
incohérentes avec les croyances alors
on n’est pas à l’équilibre ! Par exemple si supposer que mA=1 conduit à des stratégies d’équilibre
telles que le nœud B a une probabilité 1 d’être atteint, on est dans une
situation incohérente.
Autrement dit, si
l’on se donne des stratégies, (éventuellement mixtes) on peut calculer les
probabilités (associées à ces stratégies) des nœuds de l’arbre « sur la
trajectoire induite par les stratégies ». Pour les autres nœuds on peut
affecter n’importe quelle probabilité.
![]()
Définition : Equilibre Bayesien Parfait
![]() est un équilibre Bayésien parfait si :
est un équilibre Bayésien parfait si : ![]() et
et ![]()
Exercice : cliquer ici